算法-最大字串和｜默然的博客

题目描述：
首先有一串数字，共有n个，从n个数中找到连续子序列和的最大值；

解法一：暴力破解法
看到这个问题时第一时间想到的就是暴力破解法，遍历所有子序列，最终得到最大值；
e.g.
1 2 3 4 5 6 共有六个数
所有组合为
1，2，3，4，5，6
1-2，1-3，1-4，1-5，1-6
2-3，2-4，2-5，2-6
3-4，3-5，3-6
4-5，4-6
5-6
需要计算次数为：n(n+1)/2;
复杂度：n*n;

没什么难度，代码就不贴出来了；

解法二：动态规划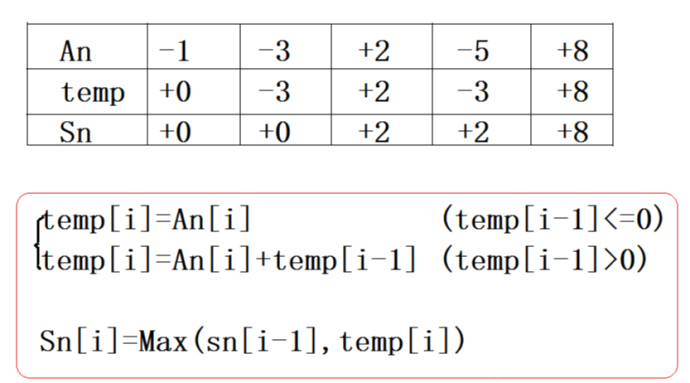

初始化变量temp=0；
最大值Sn=0；
首先输入n个数字;

当i==0时，如果An[i]<=0时，temp[i]=0,Sn=0;
****************An[i]>0时，temp[i]=An[i],Sn=An[i];
当i!=0时，
****************temp[i-1]<=0时：temp[i]=An[i];
****************temp[i-1]>0时：temp[i]=temp[i-1]+An[i];

Sn[i]=Max(Sn[i-1],temp[i]);

具体代码如下：

#include<iostream>
using namespace std;
int main()
{
    int n;
    int Sn=0;
    cin>>n;
    int a[n];
    int temp[n];

    for(int i=0;i<n;i++)
        cin>>a[i];
    for(int i=0;i<n;i++)
    {
        if(i==0)
        {
            if(a[i]<=0)
                temp[0]=0;
            else
            {
                temp[0]=a[0];
                Sn=a[0];
            }               
        }
        else
        {
            if(temp[i-1]<=0)
                temp[i]=a[i];
            else if(temp[i-1]>0)
                temp[i]=a[i]+temp[i-1];

            if(Sn<temp[i])
                Sn=temp[i]; 
        }
    }
    cout<<Sn;
}

Tony-Chen
2017.11.2
安得与君绝决，免教生死作相思

相关阅读

• 分治算法解决问题再回顾
• 算法-从第一个元素开始，计算累和的最大值