menu 首页 主站 标签 归档 关于
search more_vert
算法-排序算法总结

一言加载中...

如何分析排序算法

  1. 执行效率
  2. 内存消耗
  3. 算法稳定性：如果待排序的序列中存在值相同的元素，在排序后，相同元素的前后顺序不发生改变就是稳定。

分析排序算法

类型 名称 时间复杂度 空间复杂度 是否稳定 特殊情况
交换排序 冒泡排序 O(n²) O(1) √
快速排序 O(nlog₂n) O(1) × 基本有序最差O(n²)
选择排序 直接选择排序 O(n²) O(1) ×
堆排序 O(nlog₂n) O(1) ×
插入排序 直接插入排序 O(n²) O(1) √ 基本有序最优O(n)
Shell排序 O(n¹˙³) O(1) ×

一些特殊点

  1. 一组数据排序最坏的情况下，归并排序的时间复杂度最低(nlog₂n)
  2. 数据少量时，使用直接插入/直接选择排序。
  3. 数据量基本有序时，使用直接插入/冒泡排序。
  4. 数据量较大且位数比较少时，使用基数排序。
  5. 数据量很大时，使用O(nlog₂n)的算法：快排/堆排序/归并排序

冒泡排序

排序思想：

  1. 比较相邻的两个数据，如果前者大于后者，则进行交换位置，否则不交换
  2. 把每一个元素与相邻的数据做比较，完成后，最后的一个元素是最大数
  3. 重复上面过程，直到排序怕完成

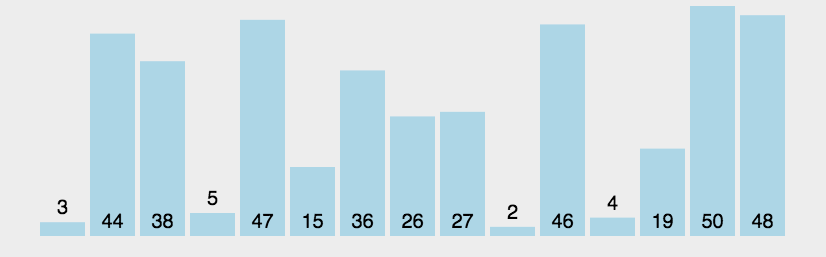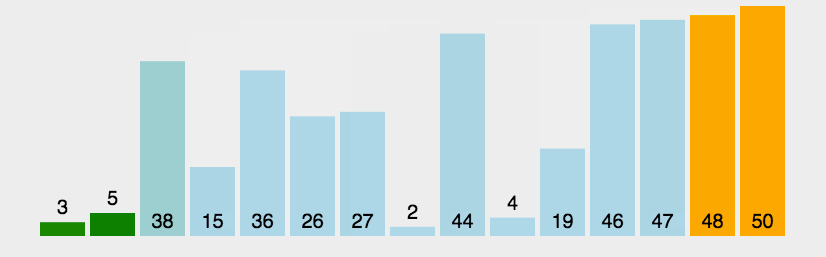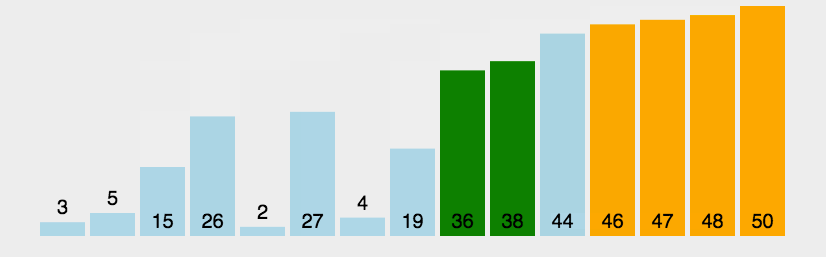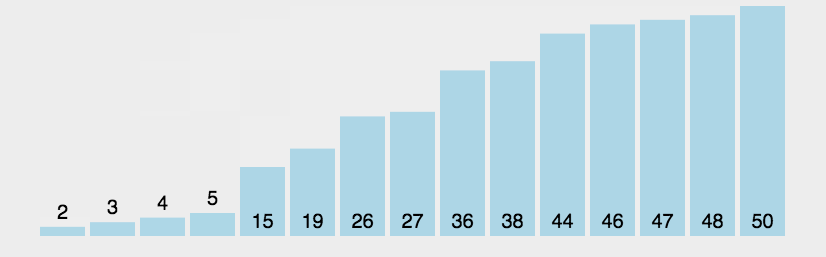
BubbleSort

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
int *BubbleSort(int a[],int size)
{
	//默认已经完成排序
	bool isSort = true;
	for (int i = 0; i < size-1; i++)
	{
		//每次默认已经排序完成
		isSort = true;
		for (int j = 0; j < size-1-i; j++)
		{
			if (a[j] > a[j + 1])
			{
				a[j] = a[j] ^ a[j + 1];
				a[j + 1] = a[j] ^ a[j + 1];
				a[j] = a[j] ^ a[j + 1];
				//当发生交换时表明排序未完成
				isSort = false;
			}
		}
		//判断如果排序完成：跳出循环
		if (isSort)
			break;
	}
	return a;
}

选择排序

排序思想：

  1. 每一趟从待排序的记录中选出最小的元素，顺序放在已排好序的序列最后，直到全部记录排序完毕。

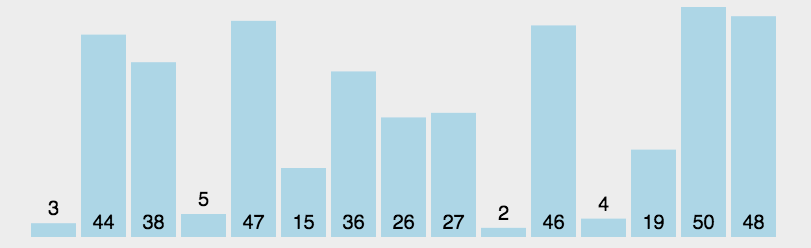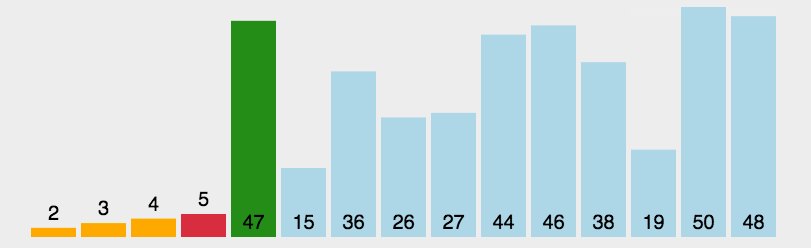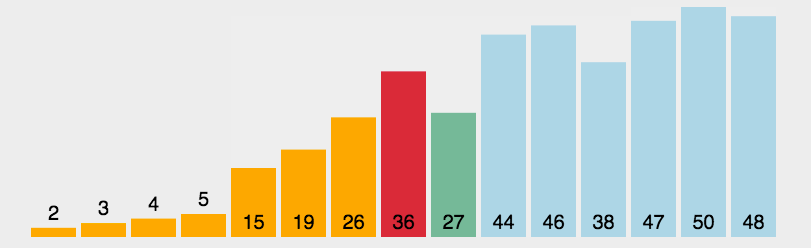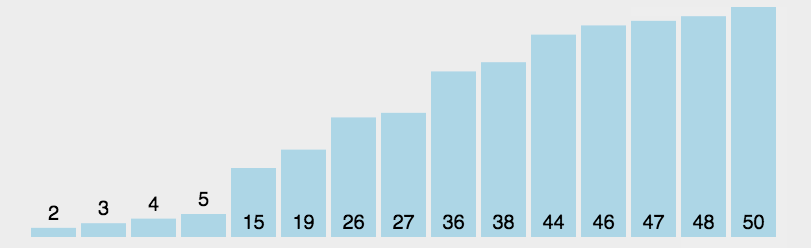
SelectionSort

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
int *SelectionSort(int a[], int size)
{
	for (int i = 0; i < size; i++)
	{
		//设置当前索引对应值为最小值
		int min_index = i;
		for (int j = i; j < size; j++)
		{
			//如果有比记录的最小值小，则记录下来
			if (a[j] < a[min_index])
				min_index = j;
		}
		if (min_index != i)
		{
			//数值交换
			Swap(a[min_index], a[i]);
		}

	}
	return a;
}

插入排序

排序思想：

  1. 从第一个元素开始，该元素可以认为已经被排序；
  2. 取出下一个元素，在已经排序的元素序列中从后向前扫描；
  3. 如果该元素（已排序）大于新元素，将该元素移到下一位置；
  4. 重复步骤3，直到找到已排序的元素小于或者等于新元素的位置；
  5. 将新元素插入到该位置后；
  6. 重复步骤2~5。

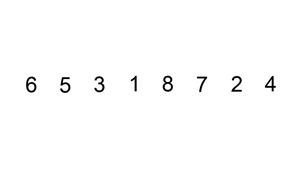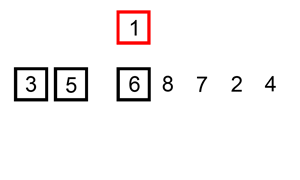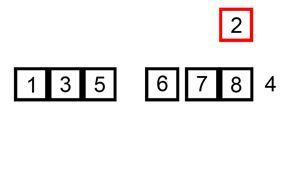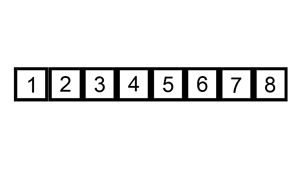
InsertionSort

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
int *InsertionSort(int a[], int size)
{
	for (int i = 1; i < size; i++)
	{
		int temp = a[i];
		int index = i-1;
		while (index>=0 && temp<a[index])
		{
			a[index + 1] = a[index];
			--index;
		}
		a[index + 1] = temp;
	}
	return a;
}

折半插入排序

排序思想：

折半插入排序是对直接插入排序的改进。

　　我们看直接插入排序的步骤简单而言其实就2步，第1步是从已经排好序的数组中找到该插入的点，第2步是将数据插入，然后后面的数据整体后移。那么直接插入排序是如何找到该插入的点的呢？是无脑式的从头到尾的遍历。问题是被插入的数组是排好序的，根本没有必要从头到尾遍历。折半插入排序就是改进了第1步——从已经排好序的数组中找到该插入的点。

　　折半插入排序是怎么做的呢？非常简单。取已经排好序的数组的中间元素，与插入的数据进行比较，如果比插入的数据大，那么插入的数据肯定属于前半部分，否则属于后半部分。这样，不断遍历缩小范围，很快就能确定需要插入的位置。这就是所谓“折半”。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
void HalfInsertionSort(int a[], int size)
{
	for (int i = 1; i < size; i++)
	{
		int l = 0;
		int h = size - 1;
		int temp = a[i];
		while (l <= h)
		{
			int mid = (l + h) / 2;
			if (temp <= a[mid])
				h = mid - 1;
			else
				l = mid + 1;
		}

		for (int j = i-1; j >= l; j--)
			a[j+1] = a[j];
		a[l] = temp;
	}
}

快速排序

排序思想：

  1. 先从数列中取出一个数作为基准数。
  2. 分区过程，将比这个数大的数全放到它的右边，小于或等于它的数全放到它的左边。
  3. 再对左右区间重复第二步，直到各区间只有一个数。

20240905 更新

关于快速排序第一次寻找基准数一直是一个谜，从大学时书籍上到网上查资料都是 “寻找一个恰当的数当作索引值”，所以很长一段时间对这个基准数都是简单粗暴的拿以一个数开头。直到一次面试被问到，后经面试官的讲解，遂得知是先进行一遍查找找到基准数后再进行快排。下面用CSharp重新实现一遍。

QuickSort

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
static void QuickSort(ref int[] array, int low, int high)
{
	// 终止条件
	if(low >= high) return;

	int pivot = QuickSortOnceForPivot(ref array, low, high);

	//递归方式，直到完成排序
	QuickSort(ref array, low, pivot - 1);
	QuickSort(ref array, pivot + 1, high);
}

static int QuickSortOnceForPivot(ref int[] array, int low, int high)
{
	//定义支点为第一个
	int pivotValue = array[low];

	while(low < high)
	{
		//从后往前比较，找一个比pivot小（或者=）的数字，放在a[l]所在位置
		while (low<high && array[high] > pivotValue) --high;
		array[low] = array[high];

		//从前往后比较，找一个比pivot大的数字，放在a[h]所在位置
		while (low <high && array[low] < pivotValue) ++low;
		array[high] = array[low];
	}
	//放入基准数
	array[low] = pivotValue;
	return low;
}

二叉排序树

数据结构-二叉排序树(三)

参考

siki 快速排序

基本排序（二）插入排序(直接插入、Shell、折半

GIF 动态图来源于网络

写博客不易，请我喝杯咖啡？

评论

arrow_upward