对于树与二叉树前面概念部分,请移步:数据结构-树与二叉树再回顾(一)
什么是二叉树的遍历:
从二叉树的根节点出发,按照某种方式依次访问二叉树中的所有节点,使每个节点都能被访问一次且只能访问一次。以下有四种遍历方式:
访问顺序
| 遍历方式 |
遍历顺序 |
| 先序遍历 |
1. 访问根节点 |
|
2. 先序遍历左子节点 |
|
3. 先序遍历右子节点 |
| 中序遍历 |
1. 中序遍历左子节点 |
|
2. 访问根节点 |
|
3. 中序遍历右子节点 |
| 后序遍历 |
1. 后序遍历左子节点 |
|
2. 后序遍历右子节点 |
|
3. 访问根节点 |
| 层序遍历 |
逐层从左到右依次遍历 |
举个栗子:
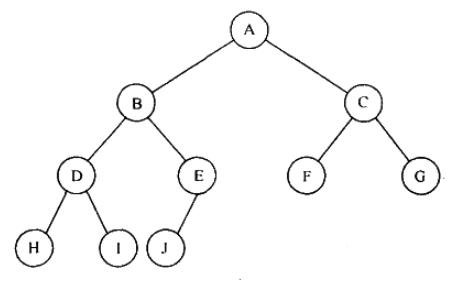
对该完全二叉树(上图)使用不同遍历方式进行输出
顺序结构
对于一个二叉树,使用顺序结构对存储时,其存储方式是按照数组形式存储的,如下图

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
| class MyTree<T>
{
private T[] data;
private int count = 0;
public MyTree(int size)
{
data = new T[size];
}
public bool Add(T item)
{
if (count >= data.Length) return false;
data[count] = item;
count++;
return true;
}
public void FirstTravel(int startIndex=0){...}
public void MiddleTravel(int startIndex=0){...}
public void LastTravel(int startIndex=0){...}
public void LayerTravel(int startIndex=0){...}
}
|
先序遍历
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
|
public void FirstTravel(int startIndex=0)
{
if (startIndex >= count) return;
int number = startIndex + 1;
Console.Write(data[startIndex]+" ");
int leftChild = number * 2;
int rightChild = number*2 + 1;
FirstTravel(leftChild - 1);
FirstTravel(rightChild - 1);
}
|
中序遍历
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
|
public void MiddleTravel(int startIndex=0)
{
if (startIndex >= count) return;
int number = startIndex + 1;
int leftChild = number * 2;
int rightChild = leftChild + 1;
MiddleTravel(leftChild-1);
Console.Write(data[startIndex] + " ");
MiddleTravel(rightChild-1);
}
|
后续遍历
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
|
public void LastTravel(int startIndex=0)
{
if (startIndex >= count) return;
int number = startIndex + 1;
int leftChild = number * 2;
int rightChild = leftChild + 1;
LastTravel(leftChild-1);
LastTravel(rightChild-1);
Console.Write(data[startIndex]+" ");
}
|
层序遍历
1
2
3
4
5
6
7
8
9
10
11
|
public void LayerTravel(int startIndex = 0)
{
for (int i = 0; i < count; i++)
{
Console.Write(data[i] + " ");
}
}
|
看下遍历结果

链式结构
对于链式结构的先序,中序,后续遍历,过于简单,只需访问根节点的左孩子,右孩子即可,最近刷力扣时遇到链式结构的层序遍历,与顺序结构的有所不同,记录下:
层序遍历
思想:
- 通过使用队列(当然也可以使用列表模拟先进后出的特性),如果根节点不为空,则将根节点入队;
- 从队列中取出一个节点(Temp);
- 如果Temp的左孩子不为空,则将Temp的左子节点入队;
- 如果Temp的右孩子不为空,则将Temp的右子节点入队;
- 如果队列不为空就重复执行2-5步,直到队列为空;
主要代码如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
|
static public int[] LevelOrder(TreeNode root)
{
Queue<TreeNode> queue = new Queue<TreeNode>();
List<int> result = new List<int>();
if (root != null)
{
queue.Enqueue(root);
}
while(queue.Count>0)
{
TreeNode node = queue.Dequeue();
if(node.left!=null)
{
queue.Enqueue(node.left);
}
if(node.right!=null)
{
queue.Enqueue(node.right);
}
result.Add(node.val);
}
return result.ToArray();
}
|
TonyChenn
2018.10.18




