什么是二叉排序树?
二叉排序树。又称二叉查找树,对于一个非空的二叉排序树:
- 若左子树不为空,则左子树的值均小于根节点的值;
- 若右子树不为空,则右子树的值均大于根节点的值;
- 使用中序遍历,即可将数据从小到大输出;
二叉排序树的功能实现理论
插入数据
- 复制一个新的根节点CurrRoot(防止直接对根节点进行操作)
- 如果currRoot为空,那么将添加的新节点赋值给CurrRoot节点
- 如果CurrRooot不为空:比较CurrRoot节点与NewNode(新节点)值的大小
- 如果 CurrRoot的值大于NewNode(新节点)的值。判断CurrRoot的LeftChild是否为空:
- 如果CurrRoot的LeftChild节点为空,则将NewNode的值赋值给CurrRoot的LeftChild节点;
- 如果CurrRoot的LeftChild节点非空,则将CurrRoot的LeftChild节点作为CurrRoot节点,继续遍历,直到找到合适的位置
- 如果 CurrRoot的值小于等于NewNode(新节点)的值。判断CurrRoot的RightChild是否为空:
- 如果CurrRoot的RightChild节点为空,则将NewNode的值赋值给CurrRoot的RightChild节点;
- 如果CurrRoot的RightChild节点非空,则将CurrRoot的RightChild节点作为CurrRoot节点,继续遍历,直到找到合适的位置
删除数据
对叶子节点进行删除
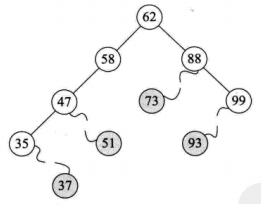
删除方式:直接进行删除
以删除51为例:
- 判断51是父节点的左孩子还是右孩子;
- 这里知道51是父节点47的右子节点
- 47节点的rightChild=null
对仅有左子树或者右子树的节点进行删除
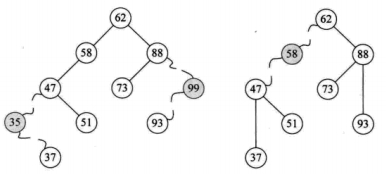
删除35节点思想:
让35节点的子节点37的父节点指向35节点的父节点47;让35的父节点47的左子节点指向35的右子节点
删除99节点思想:
让99节点的子节点93的父节点指向99节点的父节点88;让99的父节点88的右子节点指向99的左子节点
对左右节点都有的节点进行删除
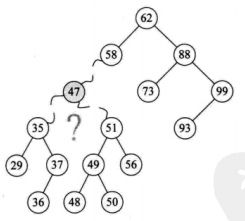
删除47节点思想:
- 将47节点的右子节点51作为临时根节点
- while循环得到当前子树的最小节点(当前根节点的左子节点的左子节点)
- 将47节点的值替换成48节点的值
- 将叶子节点48删除
二叉排序树的实现
树的节点类:TreeNode
1
2
3
4
5
6
7
8
9
10
11
12
13
| class TreeNode
{
public TreeNode Parent;
public TreeNode leftChild;
public TreeNode rightChild;
public int data;
private TreeNode() { }
public TreeNode(int item)
{
this.data = item;
}
}
|
排序二叉树
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
| class LinkTree
{
TreeNode root = null;
public void Add(TreeNode item){...}
public TreeNode Find(int item){...}
public bool Delete(int item)
{
TreeNode node = root;
while(true)
{
if (node == null) return false;
if(node.data==item)
{
Delete(node);
return true;
}
if (node.data > item)
node = node.leftChild;
else
node = node.rightChild;
}
}
private void Delete(TreeNode node){... }
public void InOrderTraverse()
{
InOrderTraverse(root);
}
private void InOrderTraverse(TreeNode tree)
{
if (tree == null) return;
InOrderTraverse(tree.leftChild);
Console.Write(tree.data + " ");
InOrderTraverse(tree.rightChild);
}
|
添加节点
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
| public void Add(TreeNode item)
{
if (root == null)
root = item;
else
{
TreeNode current = root;
while(true)
{
if(current.data>item.data)
{
if (current.leftChild == null)
{
current.leftChild = item;
item.Parent = current;
break;
}
else
{
current = current.leftChild;
}
}
else
{
if(current.rightChild==null)
{
current.rightChild = item;
item.Parent = current;
break;
}
else
{
current = current.rightChild;
}
}
}
}
}
|
节点的查找
1
2
3
4
5
6
7
8
9
10
11
12
13
| public TreeNode Find(int item)
{
TreeNode node = root;
while (true)
{
if (node == null) return null;
if (node.data == item) return node;
else if (node.data > item)
node = node.leftChild;
else
node = node.rightChild;
}
}
|
删除节点
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
| private void Delete(TreeNode node)
{
if(node.leftChild==null && node.rightChild==null)
{
if (node.Parent == null)
root = null;
else if(node.Parent.leftChild==node)
{
node.Parent.leftChild = null;
}
else if(node.Parent.rightChild==node)
{
node.Parent.rightChild = null;
}
return;
}
if(node.leftChild==null && node.rightChild!=null)
{
if (node.Parent.leftChild == node)
{
node.rightChild.Parent = node.Parent;
node.Parent.leftChild = node.rightChild;
}
else
{
node.rightChild.Parent = node.Parent;
node.Parent.rightChild = node.rightChild;
}
return;
}
if (node.leftChild!=null && node.rightChild==null)
{
if (node.Parent.leftChild == node)
{
node.rightChild.Parent = node.Parent;
node.Parent.leftChild = node.rightChild;
}
else if(node.Parent.rightChild == node)
{
node.leftChild.Parent = node.Parent;
node.Parent.rightChild = node.leftChild;
}
return;
}
TreeNode curr = node.rightChild;
while(curr.leftChild==null)
{
curr = curr.leftChild;
}
node.data = curr.data;
curr.Parent.leftChild = null;
return;
}
|
TonyChenn
2018-10-20
学算法好心累,心疼我的头发crying...





