什么是KMP算法
通俗的讲:从一个字符串中找到包含第二个字符串的开始位置。如果存在返回索引位置,否则返回-1。
问题介绍:
实现 strStr() 函数。给定一个 haystack 字符串和一个 needle 字符串,在 haystack 字符串中找出 needle 字符串出现的第一个位置 (从0开始)。如果不存在,则返回 -1。
示例:
1
2
3
4
5
6
|
输入: haystack = "abacaabacabac", needle = "abacab"
输出:5
输入: haystack = "aaaaa", needle = "bba"
输出: -1
|
来源:力扣(LeetCode))
KMP算法思路
先看个动态图

首先制作一个前缀表(PrefixTable)
前缀表的构建对于KMP算法很重要,后面会说到作用,以及如何生成。
needle 字符串的前缀表如下:
| 子串排列 |
最大公共子串 |
最大公共子串数 |
| a |
|
0 |
| ab |
|
0 |
| aba |
a |
1 |
| abac |
|
0 |
| abaca |
a |
1 |
| abacab |
ab |
2 |
| 索引(i) |
0 |
1 |
2 |
3 |
4 |
5 |
| 字符 |
a |
b |
a |
c |
a |
b |
| prefix[i] |
0 |
0 |
1 |
0 |
1 |
2 |
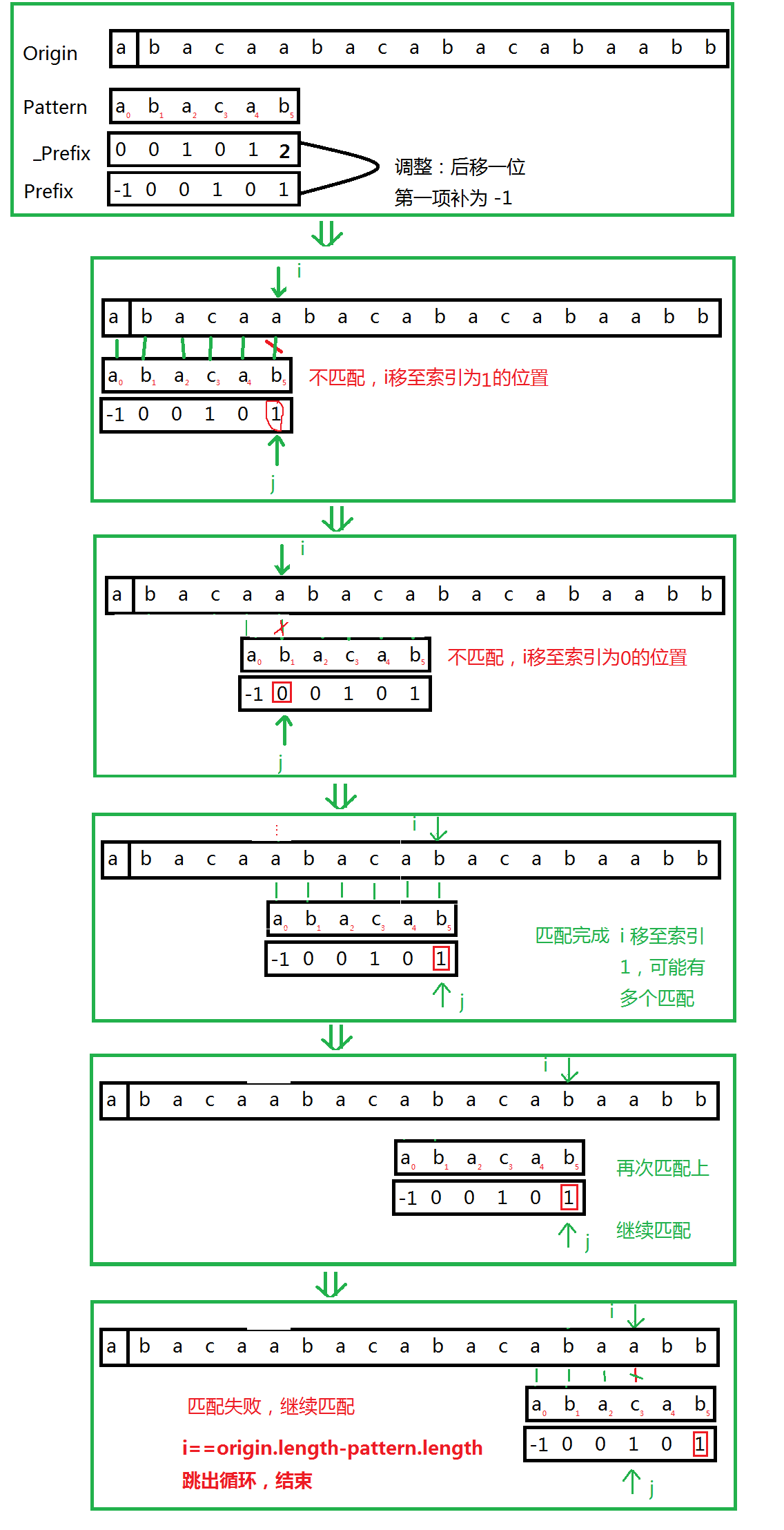
将Prefix表所有数值后移一位,第一个值补为-1,如下:
| 索引(i) |
0 |
1 |
2 |
3 |
4 |
5 |
| 字符 |
a |
b |
a |
c |
a |
b |
| prefix[i] |
-1 |
0 |
0 |
1 |
0 |
1 |
KMP匹配思想:
- 开始匹配,刚开始i=0,j=0,needle[j]与haystack[i]进行比较,直到i=5时,needle[5]与haystack[5]不相等,此时将i指向索引为prefix[5]的位置。

- 此时发现prefix[5]之前是匹配成功的,不用管,直接从索引为prefix[5]的位置继续往后比较,直到如图a->b匹配失败,就回到prefix[1]的位置
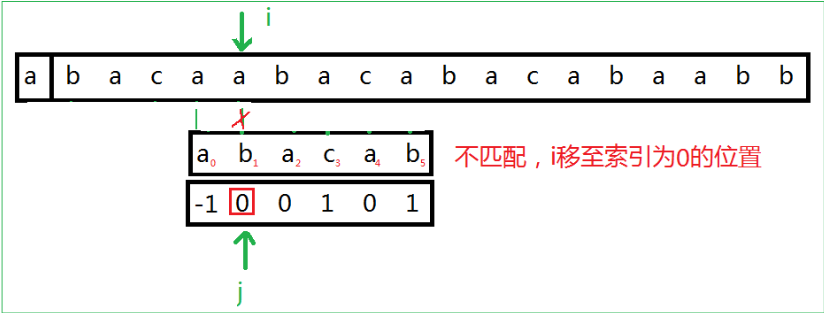
- 当出现prefix的值为-1时,那么i,j同时往后移动一位,继续上面的操作。
- 当i的值小于等于(origin.Length - pattern.Length)时跳出上面的循环。
完整过程
那么如何生成prefix表?
qaq 自己明白容易,讲出来挺难额…
代码实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
| static int KMP(string origin,string pattern)
{
if (origin.Length < pattern.Length) return -1;
else if (pattern.Length == 0) return 0;
else if (origin == pattern) return 0;
int[] prefix = new int[pattern.Length];
int pivit = 0;
for (int i = 1; i < pattern.Length; i++)
{
if (pattern[pivit] == pattern[i])
{
++pivit;
prefix[i] = pivit;
}
else
{
pivit = 0;
prefix[i]=0;
}
}
for (int i = prefix.Length - 1; i > 0; i--)
prefix[i] = prefix[i - 1];
prefix[0] = -1;
int index = 0;
int jndex = 0;
while (index <= origin.Length - pattern.Length)
{
if (jndex == pattern.Length-1)
return index = jndex;
if (origin[index] == pattern[jndex] || prefix[index]==-1)
{
++index;
++jndex;
}
else
{
jndex = prefix[jndex];
}
}
return -1;
}
|
参考





